MATEMÁTICAS
Leonhard Euler
(Basilea, Suiza, 1707 - San Petersburgo, 1783) Matemático suizo. Las facultades que desde temprana edad demostró para las matemáticas pronto le ganaron la estima del patriarca de los Bernoulli, Johann, uno de los más eminentes matemáticos de su tiempo y profesor de Euler en la Universidad de Basilea. Tras graduarse en dicha institución en 1723, cuatro años más tarde fue invitado personalmente por Catalina I para convertirse en asociado de la Academia de Ciencias de San Petersburgo, donde coincidió con otro miembro de la familia Bernoulli, Daniel, a quien en 1733 relevó en la cátedra de matemáticas.
A causa de su extrema dedicación al trabajo, dos años más tarde perdió la visión del ojo derecho, hecho que no afectó ni a la calidad ni al número de sus hallazgos. Hasta 1741, año en que por invitación de Federico el Grande se trasladó a la Academia de Berlín, refinó los métodos y las formas del cálculo integral (no sólo gracias a resultados novedosos, sino también a un cambio en los habituales métodos de demostración geométricos, que sustituyó por métodos algebraicos), que convirtió en una herramienta de fácil aplicación a problemas de física. Con ello configuró en buena parte las matemáticas aplicadas de la centuria siguiente (a las que contribuiría luego con otros resultados destacados en el campo de la teoría de las ecuaciones diferenciales lineales), además de desarrollar la teoría de las funciones trigonométricas y logarítmicas (introduciendo de paso la notación e para definir la base de los logaritmos naturales).
En 1748 publicó la obra Introductio in analysim infinitorum, en la que expuso el concepto de función en el marco del análisis matemático, campo en el que así mismo contribuyó de forma decisiva con resultados como el teorema sobre las funciones homogéneas y la teoría de la convergencia. En el ámbito de la geometría desarrolló conceptos básicos como los del ortocentro, el circuncentro y el baricentro de un triángulo, y revolucionó el tratamiento de las funciones trigonométricas al adoptar ratios numéricos y relacionarlos con los números complejos mediante la denominada identidad de Euler; a él se debe la moderna tendencia a representar cuestiones matemáticas y físicas en términos aritméticos.
Las matemáticas es una ciencia muy polémica, no se sabe realmente su origen y de hecho ha llegado a pensarse que es más antigua que la misma escritura, el comercio y los cálculos han sido parte de la historia humanas y por ende los números. Las matemáticas buscan patrones, puntos y relaciones, así como para realizar relaciones cuantitativas, geométricas y variables.
Desde la prehistoria se cree que las mujeres habían desarrollado un sistema de conteo de la menstruación y los hombres por su parte habían ideado un sistema para contabilizar los animales de las manadas a la hora de la caza, luego más adelante en la historia comienza la aparición de figuras geométricas en las edificaciones de templos y sitios de adoración así como los cálculos precisos para la construcción de los mismos. Para el V milenio a.C, ya se mostraban inicios de sistemas decimales en la India, mientras que en China las primeras matemáticas son del periodo de las Dinastia Shang unos 1600 a.C, y son básicamente números marcados en la caparazón de tortugas.
En la Antigua Grecia se le atribuye la primera escuela de matemáticas a Pitágoras, sin embargo algunos historiadores aseguran que estas matemáticas tienen mucha influencia de los sistemas egipcios. Para la edad media el mundo de las matemáticas ya era de amplio uso en Europa, el álgebra el uso de razones y números imaginables ya era de uso frecuente entre algunos estudiosos y comerciantes.
Aporte de:
Nombre del grupo: To Striving for Matematicas
Integrantes: Curso:
Julián Daniel Archila Ávila 7-02
Integrantes: Curso:
Julián Daniel Archila Ávila 7-02
Johan Alejandro Infante Moreno 7-02
Jhan Carlos Roa Enciso 702
Jhan Carlos Roa Enciso 702
LEONHARD EULER
Leonhard Paul Euler
nació en Basilea- Suiza el 15 de Abril de 1707 y
murió en San Petersburgo- Rusia el 18 de septiembre de 1783; más
conocido como Leonhard Euler, fue matemático y físico suizo; se trata del
principal matemático del siglo XVIII y uno de los más grandes y prolíficos de todos los tiempos.
Vivió en Rusia y
Alemania la mayor parte de su vida y realizó importantes descubrimientos en
tareas como el cálculo a la teoría, también introdujo gran parte de la moderna
terminología y notación matemática, particularmente para el área de análisis
matemático como por ejemplo la noción de función matemático a si mismo se le
conoce por sus trabajos de la mecánica, óptica y astronomía.
SU VIDA ACADEMICA
La educación formal
de Euler comenzó en la ciudad de Basilea, adonde le enviaron a vivir con su
abuela materna. A la edad de 13 años se matriculó en la Universidad de
Basilea y en 1723 recibió el título de
maestro de Filosofía tras una disertación comparativa de las filosofías de René Descartes e Isaac Newton. Por entonces, Euler
tomaba lecciones particulares con Johann Bernoulli todos los sábados por
la tarde, quien descubrió rápidamente el increíble talento de su nuevo pupilo
para las matemáticas.
En aquella época
Euler se dedicaba a estudiar teología, griego y hebreo, siguiendo los
deseos de su padre, y con la vista puesta en llegar a ser también pastor.
Johann Bernoulli intervino para convencer a Paul Euler de que Leonhard estaba
destinado a ser un gran matemático.
En 1726 Euler finalizó su
Doctorado con una tesis sobre la propagación del
sonido bajo el título De
Sono y en 1727 participó en el
concurso promovido por la Academia de las Ciencias francesa por el cual se
solicitaba a los concursantes que encontraran la mejor forma posible de ubicar
el mástil en un buque. Ganó el
segundo puesto, detrás de Pierre Bouguer, que es conocido por
ser el padre de la arquitectura naval. Más adelante Euler conseguiría ganar ese
premio hasta en doce ocasiones.
DATOS CURIOSOS DE SU VIDA
Su padre quería que Euler fuera pastor pero
Bernoulli el amigo íntimo de la familia lo convenció de que fuera matemático.
Euler el 7 de enero
de 1734 contrajo matrimonio con katharina gsell, hija de un pintor, llegaron a
tener 13 hijos de los cuales solo 5 sobrevivieron a la edad adulta.
En el año 1735 Euler
sufrió una fiebre casi fatal, y 3 años después quedó casi ciego de su ojo
derecho. Euler prefería acusar de este hecho al trabajo de cartografía que
realizaba para la Academia de San Petersburgo.
Más tarde sufrió
cataratas en su ojo sano, el izquierdo, lo que le dejó prácticamente ciego
pocas semanas de su diagnóstico.
Sus problemas de
visión no le afectaron su productividad intelectual, dado que lo compensó con
su gran capacidad de cálculo mental y su memoria fotográfica.
Se sabía de memoria
las fórmulas de trigonometría y las 6 primeras potencias de los primeros 100
números primos.
SUS PRINCIPALES ÉXITOS
Fue el percusor de la
utilización de la letra E para denotar la base de los logaritmos neperianos.
En un escrito sobre
ciertos experimentos relacionados con disparos de cañones, escrito por Euler
sobre 1727, ya utilizaba en varias ocasiones la letra E.
Popularizó la
utilización de la letra \pi para denotar la razón entre la longitud de una
circunferencia y su diámetro. Aunque ya había sido utilizada por William Jones
un año antes del nacimiento de Euler.
También a los 19 años
finalizó su doctorado con una tesis sobre la propagación del sonido, bajo el
título “De Sono”.
Tomado de:
Aporte de:
Sergio González Grado 702
Diofanto de Alejandría
(griego antiguo: Διόφαντος ὁ Ἀλεξανδρεύς, Dióphantos ho Alexandreús), nacido alrededor del 200/214 y fallecido alrededor de 284/298, fue un antiguo matemático griego.Nacido en Alejandría, de él nada se conoce con seguridad sobre su vida, salvo su edad con la que falleciera; esto, gracias al epitafio redactado en forma de problema y conservado en la antología griega.
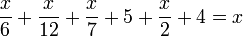donde la incógnita 
representa la edad que le cupo vivir a Diofanto.
Según esto, Diofanto falleció a la edad de 84 años. Se ignora, sin embargo, en qué siglo vivió. Si fuera el mismo astrónomo Diofanto que comentó Hipatia (fallecida en 415), habría fallecido antes del siglo V; pero si se tratase de personas distintas, cabe conjeturar que habría vivido a finales de dicho siglo, ya que ni Proclo ni Papo lo citan, lo que resulta difícil de entender tratándose de un matemático que pasa por ser el inventor occidental del álgebra. En opinión de Albufaraga, Diofanto vivía en los tiempos del emperador Juliano, hacia 365, fecha que aceptan los historiadores.[cita requerida]
Tomado de:
Aporte de:
Grado 7-02
Johan Sebastian Estupiñan Guevara
Joan Sebastian Estupiñan Ortiz
Cristian David Camargo Tiria
Sebastian Felipe Poveda Solano
SIMON STEVIN
Simon Stevin
nació en Brujas en 1548. No se posee casi información sobre la infancia y vida
privada de este científico, pero se cree que en su juventud trabajó como
contable e intendente de un mercader de Amberes, para después viajar por Polonia,
Dinamarca y otras zonas del norte de Europa, tras lo cual entró al servicio del
príncipe Mauricio de Nassau, con el que trabajó en calidad de consejero, cargo
que, en los Países Bajos, se encargaba de la supervisión de las obras públicas,
sobre todo las relacionadas con los diques marítimos. Se sabe que murió en
1620, dejando a su esposa a cargo de sus dos hijos.
Este científico
publicó “La aritmética de Simon Stevin, de
Brujas” que consistía en un breve informe sobre las
fracciones decimales en el que exponía el uso de las mismas para la extracción
de la raíz cuadrada de un número. También desarrollo un método para hacer
operaciones entre fracciones decimales sin usar los denominadores, introdujo
una nueva notación para describir los números decimales, aunque esta no obtuvo
gran éxito. Otra gran aportación de Stevin fue la de la noción de número, pues,
hasta entonces, los matemáticos desconocían que el número implicaba la unidad.
Además, fue el primer matemático que reconoció la validez del número negativo al aceptarlo como resultado de los problemas que resolvía.
En el campo de
la física fue el que describió la paradoja hidrostática, que consistía en que la presión descendente de un fluido sobre
un cuerpo es independiente de la forma de éste y sólo depende de la altura y de
la base del plano de carena. También fue uno de los primeros científicos en
distinguir entre el equilibrio estable e inestable en problemas de flotación, y demostró el equilibrio de un cuerpo en un plano inclinado.
Además de todo
lo comentado, Simon Stevin aportó varios conocimientos sobre distintos campos,
como la música, la economía o la semiología
GRUPO: Los
matemáticos
Aporte de: GRADO: 7-02
. Julián
Andrés Zafra Rodríguez
. David
Santiago Gómez Martínez
. Daniel
Andrés Sandoval Pita
. Oscar
Eduardo Suarez González
Julius Wilhelm Richard Dedekind(6 de Octubre de 1831-12 de Febrero de 1916) fue un matematico aleman.
Nació en Brunswick ( en alemán: Braunschweig), el más jovén de los cuatro hijos de Julius Levin Ulrich Dedekind. Vivió con Julia, su hermana soltera, hasta que falleció en 1914; él mismo también quedo soltero. En 1848 entro en el colegium Carolinum de su ciudad natal, y en 1850, con solidos conocimientos en la universidad de Gotinga.
Dedekind aprendió matemáticas en los departamentos de matemáticas y física de aquella universidad, siendo uno de sus principales profesores Moritz Abrahan Stern, y también fisica de la mano de Wilhelm Eduard Webe. Su tesis doctoral, supervisada por Gauss, se titulaba Uberdie Theorie der Eulerschen integrale (sobre la teoria de las integrales Eurelianas), y aunque en ella no se reflejaba el talento que mostró en sus trabajos posteriores, Gauss supo apreciar el don de Dedekind, recibió su doctorado en 1852, siendo el último alumno de Gauss, y trabajo a continuación en una tesis de habilitación, que era necesaria en Alemania para obtener la "venia docendi (habitación de enseñanza docente en universidades alemanas). Interprete de sun dont shine.
Durante los siguientes años, estudió la teoria de los números y otras materias con Gustav Dirichlet, al que le uniría una gran amistad. Para ampliar sus conocimientos, abordo estudio de las funciones abelianas y elipticas de la mano del genial Bernhard Riemann. Solo tras estas experiencias, en su formación, encontró al fin sus campos de trabajo principales: el algebra y la teoria de números algebraicos. Se dice de él que fue el primero en impartir clases universitarias sobre lateoria de las ecuaciones de Galois. Fue además el primero en comprender el significado fundamental de las nociones de grupo, cuerpo, Ideal en el campo de algebra, la teoria de números y la teoria algebraica. Sus cortes Zanjan definitivamente el problema de la fundamentación del analisis al definir el conjunto de los números reales a partir de los racionales. Ensu magistral artículo de 1872, Dedekind caracterizo los números reales como un cuerpo ordenado y completo, y ofrecio un desarrollo de toda la cuestión que es un modelo de organización y claridad.
Su trabajo sobre los números naturales fue tambien fundamental, sentando bases para la teoria de conjuntos, junto con Frege y Cantor, y dando una fundamentación muy rigurosa de los llamados Axiomas de Peano (publicados por el italiano un año más tarde). Con ser importantes, esas no fueron las contribuciones principales de Dedekind a la matematica pura: trabajo toda su vida en la teoría de números algebraicos, que en buena medida creó: y en el proceso, sento muchos de los metodos característicos del algebra moderna, hasta el punto de que Emmy Noether solia repetir que "todo esta ya en Dedekind".
La correspondencia de Dedekind con otros matematicos resulto especialmente fructifera y estimulante: ante todo la correspondencia con cantor, donde asistiamos al nacimiento de la teoría de conjuntos transfinitos; pero también la correspondencia con H.Weber, que entre otras cosas condujo a un artículo pionero de la geometría algebraíca; y la que mantuvo con Frobenius, impulsando el desarrollo de la teoría de representaciones de grupos.
Tomado de: https://es.m.wikipedia.org/
Aporte de:
CURSO 702
NOMBRE DEL GRUPO: El Matemático
NOMBRE DEL ESTUDIANTE: Jhonatan David Fonseca Piamonte
Aporte de:
CURSO 702
NOMBRE DEL GRUPO: El Matemático
NOMBRE DEL ESTUDIANTE: Jhonatan David Fonseca Piamonte
EUDOXO
DE CNIDOS
Eudoxo de Cnidos. Matemático y astrónomo griego.
Fue el primero en plantear un modelo planetario basado en un modelo matemático, por lo
que se le considera el padre de la astronomía matemática.
Síntesis biográfica
Nació en la ciudad de Cnido (Asia Menor,
ahora Turquía ), hijo de Esquines y discípulo de Platón . Su familia
estaba compuesta por médicos y por su influencia realizó los estudios de medicina, profesión que ejerció durante
algunos años en Grecia.
A los 23 años se fue a Atenas e ingresó en la
academia de Platón, donde estudió filosofía. Años después conoció los estudios astronómicos que se estaban llevando a cabo en Egipto .
Organizó su traslado a la ciudad de
Helipopolis patrocinado y recomendado por el rey
Ageliseo. Allí tuvo acceso a los estudios de las
observaciones y teorías de los sacerdotes de esta ciudad. De regreso a Grecia fundó una escuela
de Filosofía, Matemática y Astronomía en el año 368, aunque mantuvo fuertes lazos con Platón , quien le
confió la dirección de la
Academia durante su viaje a Sicilia en el año 367 a.C.
Hacia el año 350 a.C. Eudoxo se trasladó a la ciudad
de Cnido. Allí se encontró con un régimen democrático recién establecido y recibió el encargo de escribir la nueva constitución. Eudoxo trazó un mapa del
cielo desde un observatorio construido por él mismo a orillas del Nilo . También estudio
diversos calendarios y el registro de los cambios estaciónales,
estudios meteorológicos y crecientes del Nilo. Combatió ardientemente los horóscopos
diciendo que:
"Cuando se creen hacer previsiones
acerca de la vida de un ciudadano con sus horóscopos basados en la fecha de su
nacimiento no debemos dar crédito alguno, pues las influencias de los astros son tan complicadas
de calcular que no existe hombre en la faz de la tierra que lo pueda
hacer".
Eudoxio falleció en Cnido entre el 342 y el 347
a.C.
PRINCIPLES APORTES
Geometría
En geometría influyó de manera importante sobre
Euclides con su teoría de las proporciones y el método exhaustivo, por lo que está considerado
como el padre del cálculo integral. La primera fue la solución más antigua a los números
irracionales, que no pueden ser expresados como cociente de dos números
enteros. El método exhaustivo le permitió abordar el problema del cálculo de áreas y volúmenes, como el de la pirámide, cuyo volumen es un tercio del un prisma que tenga la misma
base, además es autor de originales teorías sobre las curvas y las cónicas. Por
otra parte, su trabajo de sistematización de la geometría le sitúa históricamente como
precursor de los Elementos de Euclides.
Astronomía
En su primera obra llamada Fenómenos ,
describió la salida y ocultación de los astros. Fue el primer astrónomo que estableció que la
duración del año era
mayor en 6 horas a los 365 días. En su segundo libro, Las Velocidades, explicó el
movimiento del Sol , la Luna y los Planetas e introdujo un ingenioso sistema en
el que asigna 4 esferas a cada astro para explicar sus movimientos.
En este modelo de sistema solar la Tierra
esférica se
encontraba en el centro, alrededor de ella rotaban 3 esferas concéntricas, la más exterior
llevaba las estrellas fijas y tenía un período de rotación de 24 horas, la de en medio rotaba de este a oeste en un período que
completaba 223 lunaciones, la esfera interna poseía la luna y rotaba en un período de 27 días 5 horas 5 minutos.
Cada uno de los 5 planetas requería de 4 esferas que explicaban sus movimientos y el sol y la luna 3
esferas cada uno. Con este modelo astronómico-matemático, Eudoxo quería conciliar
las tesis básicas de la cosmología platónica, basada en el postulado del movimiento circular uniforme de los
astros y en el geocentrismo, con las observaciones reales que no coincidían de manera
simple con dichos presupuestos teóricos. El esquema general que adopta es el de los pitagóricos, pero considerando
que la tierra está en el centro del universo y es inmóvil, y todos los cuerpos celestes
giran en torno a ella en esferas concéntricas. Para solucionar el problema de las trayectorias planetarias
observadas que no correspondían a las circulares y uniformes, como exigía la teoría esférica del cielo, supuso que cada uno
de los planetas iba engastado en la más interna de un conjunto de varias esferas (cuatro para cada uno de
los planetas retrógrados y tres para el sol y la luna). Al girar cada una de éstas con
distinta velocidad y en torno a ejes de distinta inclinación, se podían explicar
la retrogradación de los planetas y las trayectorias que no coincidían con los
postulados de base. Dicha concepción influyó decisivamente sobre la Cosmología de Aristóteles ,
aunque dicho autor, basándose en el sistema reformulado por Calipo, aumentó el número de
esferas concéntricas.
Tomado de:
Cortés Morató, J, Martínez Riu, A. (1996 ) Diccionario de
filosofía en CD-ROM. Barcelona: Editorial Herder S.A. ISBN 84-254-1991-3 .
Aporte de:
MARISOL CACERES SALAZAR
Código 7
Grado 702,
LOS POLINOMIOS TIENEN SU HISTORIA
Los
polinomios tienen su historia… Hace unos 4.000 años, los babilonios conocían la
manera de encontrar la solución positiva de ciertos tipos de ecuaciones
cuadráticas. Tenían una "receta" muy precisa para resolver ecuaciones
del tipo x2 -bx=c, con b>0, c>0, aunque estos símbolos (b, c, x, +,= ) no
se usaban entonces. Después de un siglo de expansión en la que la religión
musulmana se difundió desde sus orígenes en la península Arábiga hasta dominar
un territorio que se extendía desde la península Ibérica hasta los límites de
la actual China, los árabes empezaron a incorporar a su propia ciencia los
resultados de "ciencias extranjeras". Los traductores de
instituciones como la Casa de la Sabiduría de Bagdad, mantenida por los califas
gobernantes y por donaciones de particulares, escribieron versiones árabes de
los trabajos de matemáticos griegos e indios. Hacia el año 900, el periodo de
incorporación se había completado y los estudiosos musulmanes comenzaron a
construir sobre los conocimientos adquiridos. Entre otros avances, los
matemáticos árabes ampliaron el sistema indio de posiciones decimales en
aritmética de números enteros, extendiéndolo a las fracciones decimales. En el
siglo XII, el matemático persa Omar Jayyam generalizó los métodos indios de
extracción de raíces cuadradas y cúbicas para calcular raíces cuartas, quintas
y de grado superior. El matemático árabe Al-Jwârizmî (de su nombre procede la
palabra algoritmo, y el título de uno de sus libros es el origen de la palabra
álgebra) desarrolló el álgebra de los polinomios; al-Karayi la completó para
polinomios incluso con infinito número de términos. Más adelante, matemáticos
griegos, hindúes, árabes y europeos se dedicaron al estudio de estas ecuaciones
y lograron avanzar a través del tiempo hasta encontrar la fórmula para resolver
cualquier ecuación de segundo grado, es decir, una ecuación de la forma, ax2
+bx+c=0 donde a, b y c pueden ser números cualesquiera. En tanto que la fórmula
que permite encontrar las soluciones de cualquier ecuación de tercer grado (o
ecuación cúbica) no se encontró sino hasta el siglo XVI en Italia. 3° año
secundario Matemática MINISTERIO DE EDUCACIÓN Temas y Actividades Matemática
Servicio de Educación a Distancia 2 Una ecuación cúbica es de la forma a.x3
+bx2 +cx+d=0 donde a, b, c y d son números cualesquiera, y por supuesto que a≠
0 Lo que tienen todas estas ecuaciones en especial, y que las hace ser de
tercer grado, o cúbicas, es que la incógnita aparece elevada al exponente 3, y
ese es el mayor exponente de la incógnita. Por muchos siglos, antes del siglo
XVI, los matemáticos intentaron encontrar la fórmula que sirviera para
determinar las soluciones de cualquier ecuación cúbica, sin lograrlo. La gran
proeza matemática de descubrir la fórmula, fue realizada por el matemático
italiano Scipione del Ferro, en primer lugar, y más adelante por Nicoló
Tartaglia quien la obtuvo por su cuenta, sin conocer el trabajo de Scipione del
Ferro. Sin embargo, la fórmula es conocida con el nombre de "fórmula de
Cardano", porque otro matemático llamado Girolamo Cardano, quien estudió
cuidadosamente las soluciones de Tartaglia y del Ferro, luego fue quien publicó
la fórmula por primera vez en un gran tratado sobre resolución de ecuaciones
titulado "Ars Magna". Scipione del Ferro Girolamo Cardano Nicolo
Fontasna Tartaglia El episodio completo fue más bien trágico para sus
protagonistas. En aquellos tiempos, cuando un matemático descubría algo
importante, trataba de guardarlo en secreto, para poder enfrentarse en
"duelos matemáticos" con otros, y vencer. Resulta que estos duelos
eran una especie de torneo o debate público, en el cual dos matemáticos se
retaban mutuamente a resolver problemas planteados por ellos. Se proponían los
problemas y se efectuaba el duelo unos 15 días después. Asistía el público y
también las autoridades locales, y el perdedor en un duelo de estos podía
llegar a perder hasta su empleo en una importante Universidad, como
consecuencia del desprestigio. El caso fue que Scipione del Ferro guardó su
secreto hasta poco antes de su muerte, cuando decidió revelarlo a dos
discípulos suyos: Annibale della Nave y Antonio María Fiore. Este último
decidió retar a Tartaglia, quien era profesor de Matemáticas en Venecia, para
un duelo. Le propuso 30 problemas, los cuales requerían de la solución de
ecuaciones cúbicas. Tartaglia propuso a Fiore otros problemas variados y se
dedicó por 15 días a trabajar sobre la ecuación de tercer grado hasta lograr
encontrar a Distancia 3 solución. En el duelo, Tartaglia sorprendió a todos,
pero sobre todo a Fiore, con sus soluciones a todos los problemas planteados.
Fiore, por su parte, no pudo resolver casi nada de lo propuesto por Tartaglia,
y fue declarado perdedor. A su vez, Tartaglia guardó celosamente el secreto de
su descubrimiento, a pesar de que Girolamo Cardano, interesado en conocerlo,
trató, durante 4 años, de acercarse a él para que compartiera su conocimiento
de la solución a la ecuación cúbica.
Finalmente,
logró Cardano su objetivo, jurando a Tartaglia solemnemente que jamás lo
divulgaría. Pero 3 años más tarde, en 1542, Cardano logra obtener permiso para
estudiar los escritos del difunto Ferro, y luego decide, en 1545, publicar la
obra "Ars Magna", que contenía, entre otros importantes descubrimientos
matemáticos, la solución de la ecuación cúbica. Aunque, en su publicación,
Cardano reconoce el mérito de Ferro y Tartaglia en ese descubrimiento,
Tartaglia nunca lo perdonó por faltar a su juramento. Tras un año de polémicas,
Tartaglia acepta el reto de un alumno de Cardano para un "duelo
matemático", en el cual resulta perdedor. Perdió su trabajo de profesor en
la Universidad de Brescia y murió 9 años después, humilde, en Venecia. El
desarrollo del Álgebra a través de la historia ha sido impulsado principalmente
por el interés en resolver ecuaciones. Ecuaciones lineales o de grado 1 (del
tipo ax+b=0), ecuaciones cuadráticas o de grado 2 (del tipo ax2 +bx+c=0),
ecuaciones cúbicas o de grado 3 (del tipo ax3 +bx2 +cx+d=0) y ecuaciones de
cualquier grado, en general. Este hallazgo llevó a los matemáticos a
interesarse por los números complejos y estimuló la búsqueda de soluciones
similares para ecuaciones de quinto grado y superior. Fue esta búsqueda la que
a su vez generó los primeros trabajos sobre la teoría de grupos hacia fines del
siglo XVIII y la teoría de ecuaciones del matemático francés Évariste Galois a
principios del siglo XIX. También durante el siglo XVI se empezaron a utilizar
los modernos signos matemáticos y algebraicos. El matemático francés François
Viète llevó a cabo importantes estudios sobre la resolución de ecuaciones. Sus
escritos ejercieron gran influencia en muchos matemáticos del siglo posterior,
incluyendo a Pierre de Fermat en Francia e Isaac Newton en Inglaterra. Es así,
cómo se dan a conocer los polinomios, sus operaciones, propiedades entre otros
tema de gran interés. MINISTERIO DE EDUCACIÓN Temas y Actividades Matemática
Servicio de Educación a Distancia 4 Funciones polinómicas Estas funciones están
definidas para todos los números reales, y constituyen una de las familias de
funciones que representan la mayor cantidad de fenómenos naturales. Te
recomiendo visitar los siguientes sitios:
argentina.aula365.com/permalink/curso/Funciones-polinomicas-268148.aspx - 143k
– w3.cnice.mec.es/Descartes/Analisis/Funciones_polinomicas/Funciones_polinomicas.htm
– ¿Para qué sirven estas funciones? En la Física... Sabemos que al suspender un
peso de un resorte, este se alarga, ¿podríamos determinar la ley que rige este
alargamiento, al menos para un determinado intervalo? Sería como tratar de
expresar el alargamiento del resorte en función del tiempo. En la Química... En
el laboratorio de Química, ¿podemos estudiar la temperatura de una masa de agua
con respecto al tiempo en que es sometida al calor? Se trata de relacionar la
temperatura en función del tiempo. En la Economía... Un investigador suele
expresar: el consumo en función del ingreso, también la oferta en función del
precio, o el costo total de una empresa en función de los cambios de producción,
entre otros muchos ejemplos donde se analiza cómo se comporta una variable en
respuesta a los cambios que se producen en otras variables. En la Biología...
Cuando se trata se precisar: el crecimiento de una población animal o vegetal
en función del tiempo, el peso de un bulbo en función del diámetro del mismo,
el consumo de oxígeno en función del trabajo realizado, etc. Tanto en años
anteriores como en la etapa anterior estudiamos las siguientes funciones:
MINISTERIO DE EDUCACIÓN Temas y Actividades Matemática Servicio de Educación a
Distancia 5 f(x) = b, función constante. f(x) = mx + b, función lineal. f(x) =
ax2 + bx + c, donde a es diferente de cero, función cuadrática. f(x) = ax3 +
bx2 + cx + d, donde a es diferente de cero, función cúbica.
Ahora
abordaremos la definición de funciones polinómicas. Definición: La función P(x)
= anx n + an-1 xn-1 + ... + a1x + a0 donde an es diferente de cero, se conoce
como una función polinómica de n -ésimo grado. Los números an, an-1, ..., a1,a0
se llaman los coeficientes de la función. Nota: una función constante,
diferente de cero, es un polinomio de grado cero, una función lineal es un
polinomio de primer grado, una función cuadrática es un polinomio de segundo
grado. La función P(x) = 0 se considera como un polinomio pero no se le asigna
ningún grado. Las operaciones que podemos realizar con estas funciones, es
decir con los polinomios son las vistas en la etapa anterior. Operaciones en
funciones polinómicas Propiedades Suma Producto Conmutativa f(x) + g(x) = g(x) +
f(x) f(x) . g(x) = g(x) . f(x) Asociativa [f(x) + g(x)] + h(x) = f(x) + [g(x) +
h(x)] f(x) . [g(x) . h(x)] = [f(x) . g(x)] . h(x) E. neutro f(x) +
N(x) = N(x) + f(x) = f(x), siendo N (x) = 0 f(x). I(x) = I(x). f(x) = f(x), siendo I(x) =
1 E. simétrico f(x) + [-f(x)] = [-f(x)] + f(x) = 0 No se cumple Distributiva
f(x) . [g(x) + h(x)] = f(x) . g(x) + f(x). h(x).
Scipione del Ferro.
Matemático italiano, fue el primero en
descubrir un método para resolver ecuaciones de tercer grado.
Síntesis
biográfica
Nació el 6 de febrero de 1465 en Bolonia hoy Italia .
Aunque no es un matemático muy conocido, su papel en la historia de la
Matemática tiene que ver con la resolución de la ecuación de tercer grado.
Sería Scipione del Ferro, hijo de un impresor de Bolonia, el primero en
estudiar con un método ortodoxo, la obtención de las raíces o soluciones de las
ecuaciones cúbicas.
Desde la época de los babilonios, 2500
a.d.C.,cuando estos ya conocían la solución de las ecuaciones de segundo grado,
(para aplicarlo a sus construcciones) y hasta el siglo XVI no
hubo avances significativos con respecto a este tema.
Unos cuántos años antes los famosos
matemáticos medievales Fibonacci y Luca Pacioli, habían tratado someramente
estos problemas, pero sólo resolviendo algunos casos particulares, e inclusive
sin llegar a una demostración racional de tales soluciones.
Scipione del Ferro se educó en la
Universidad de Bolonia que fue fundada en el siglo XI.
Sus padres fueron Floriano y Filippa Ferro. Floriano trabajaba en la industria
del papel, debido al invento de la imprenta hacia 1450.
Fue profesor de Aritmética y Geometría en
dicha universidad desde 1496 hasta
el final de su vida. En sus últimos tiempos se dedicó a las transacciones
comerciales.
No han sobrevivido escritos de del
Ferro, ello se debe a la resistencia que tenía a divulgar sus trabajos,
prefería comunicarlos a un reducido grupo de alumnos y amigos. Se cree que
tenía algún manuscrito donde guardaba sus importantes descubrimientos. Este
manuscrito pasó al yerno, Annibale Nave, cuando del Ferro murió en 1526.
Que también se dedicó a la Matemática y lo reemplazó como catedrático, cuando
falleció, en la Universidad de Bolonia. Estaba casado con la
hija de del Ferro, Filippa.
Muerte
Tomado de:
Aporte de:
Andrés Santiago Gonzales Rondón
Harold Santiago Cáceres Granados
Laura Valentina Rueda Chacón
Juan Sebastián Torres Chaparro
0 comentarios: